Assignatures
Descripcions resumides de les assignatures
Càlcul
El càlcul infinitesimal és la base de molts models i tècniques de la ciència i l’enginyeria, en particular l’optimització, que és cabdal en aprenentatge automàtic. El curs introdueix conceptes bàsics al voltant de les dues operacions bàsiques: La diferenciació i la integració.
Temari
- Nombres
- Funcions elementals
- Funcions de diverses variables
- Límits i continuïtat
- Derivades
- Integració
Més informació a la guia de l'assignatura.
Àlgebra
En aquesta assignatura s’introduiran els conceptes d’àlgebra lineal necessaris per a desenvolupar l’anàlisi de dades i la seva visualització al llarg del grau. Estudiarem conceptes algebraics des del punt de vista de l’àlgebra matricial, però també des del geomètric i el numèric. Es posarà èmfasi en exemples provinents del camp de la computació, de la modelització de dades, i del tractament d’imatges.
Temari
- Matrius
- Espais vectorials
- Aplicacions lineals
- Diagonalització
- Producte escalar
- Descomposició en valors singulars
- Matrius estocàstiques
Més informació a la guia de l'assignatura.
Matemàtica Discreta i Lògica
La matemàtica discreta és la branca de les matemàtiques amb una relació més directa amb la teoria de la computació; de fet, el seu gran desenvolupament al segle passat es deu en bona part a l’aparició de la informàtica. El curs introdueix diverses matèries interrelacionades –lògica, aritmètica, combinatòria i teoria de grafs—, que són el fonament de la matemàtica discreta. La presentació dels temes farà èmfasi en els aspectes algorísmics i computacionals.
Temari
- Càlcul proposicional i de primer ordre
- Formes normals
- Aritmètica d’enters i de polinomis
- Enumeració bàsica
- Equacions recurrents i funcions generadores
- Probabilitat discreta
- Grafs i digrafs
- Arbres. Arbre generador minimal
- Coloració de grafs. Algorismes
- Fluxos en xarxes i aparellaments
Més informació a la guia de l'assignatura.
Algorísmia i Programació I
El curs presenta els elements d’un llenguatge de programació de computadors i els fonaments bàsics d’algorísmia per treballar amb dades escalars i estructurades. Durant el curs s’adquiriran els coneixements per tractar problemes de càlcul de petita i mitjana complexitat.
Temari
- Elements bàsics d’un llenguatge de programació: instruccions i tipus de dades.
- Funcions.
- Algorismes bàsics amb dades escalars.
- Recursivitat.
- Vectors i algorismes sobre vectors.
- Anàlisi de complexitat d’algorismes.
- Ordenació de vectors.
- Matrius i algorismes sobre matrius.
- Estructures de dades.
- Algorismes numèrics bàsics.
- Algorismes combinatoris.
- Realització de pràctiques amb C++ i python.
Més informació a la guia de l'assignatura
Àlgebra i Càlcul II
En aquesta assignatura s’ampliaran alguns conceptes vistos a les assignatures prèvies però pels casos multidimensionals. Estudiarem conceptes geomètrics útils de cara a les visualitzacions de dades i també veurem el concepte d’aproximació d’un conjunt de dades via mínims quadrats i transformades de Fourier. L’evolució temporal d’un problema s’estudiarà a partir de les equacions diferencials.
Temari
- Geometria Afí
- Aproximació Mínim Quadràtica
- Integració Múltiple
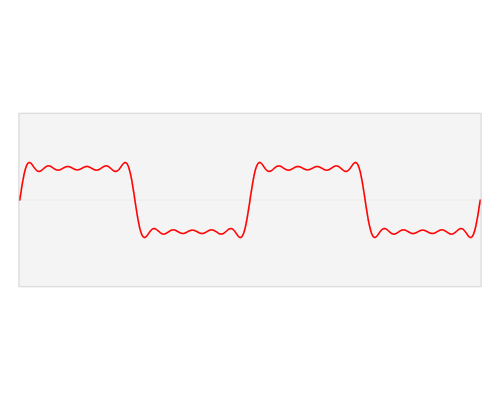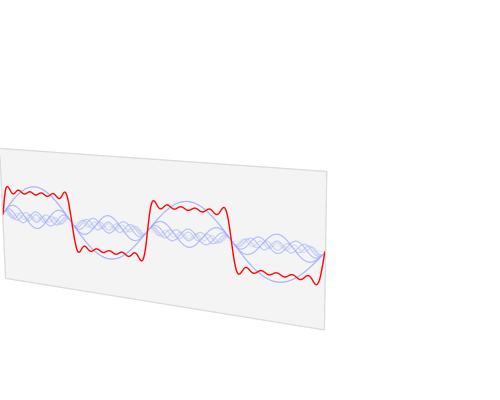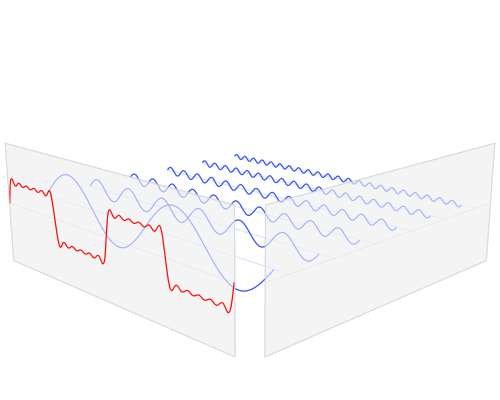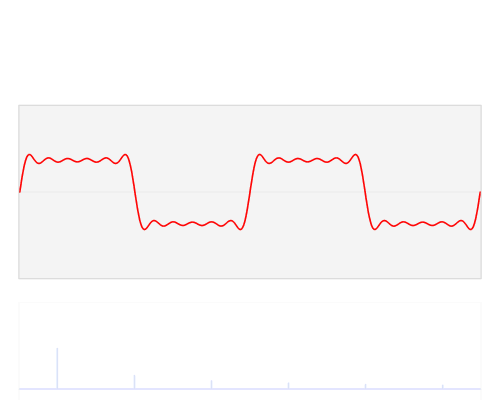
- Transformada de Fourier
- Equacions Diferencials
Més informació a la guia de l'assignatura
Probabilitat i Estadística I
L'assignatura permet adquirir les bases i habilitats en les tècniques estadística i de modelització que són necessàries per al desenvolupament de les aplicacions en enginyeria de dades. Es proporciona el marc conceptual i les habilitats instrumentals en teoria de la probabilitat, estadística i modelització de fenòmens probabilistes.
Temari
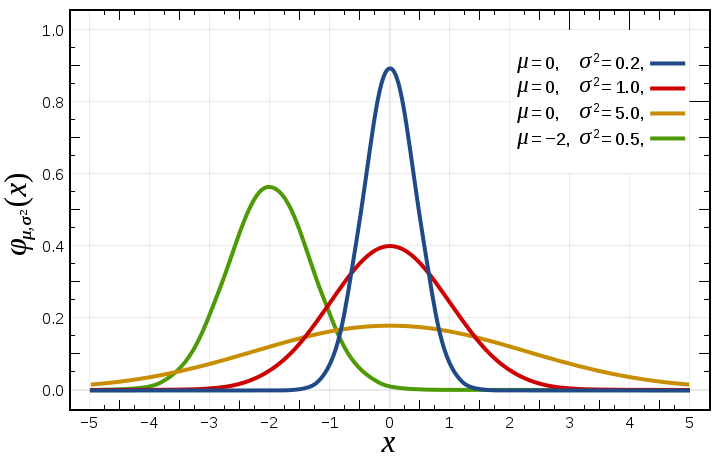
- Espais de probabilitat i variables aleatòries.
- Variables aleatòries.
- Vectors aleatoris.
- Sumes de variables aleatòries.
- Població i mostra.
- Estimació puntual.
- Intervals de confiança.
- Contrastos d'hipòtesi.
Més informació a la guia de l'assignatura
Computadors
El curs presenta els coneixements sobre l’estructura dels computadors: processadors, jerarquia de memòria, elements d’entrada/sortida, emmagatzament de dades I els fonaments de la programació a baix nivell dels computadors. També incorpora els coneixements bàsics sobre codificació de dades, l’estructura dels programes i llibreries, nivells d’execució usuari i sistema operatiu, sistemes de fitxers i interpretació i compilació.
Temari
- Codificació de les dades: naturals, enters, i coma flotant. Error relatiu i absolut
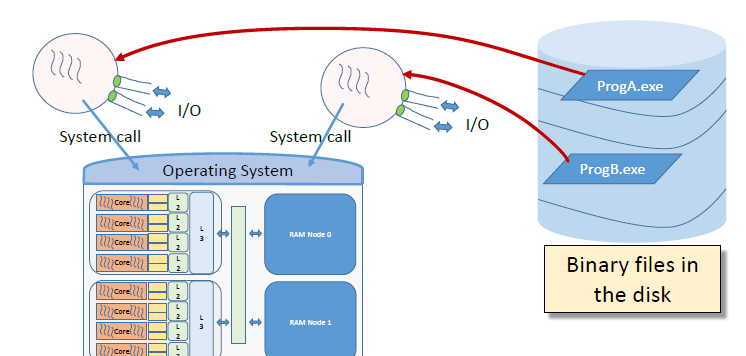
- Processadors i jerarquia de memòria. Localitat de dades
- Nivells d’execució usuari i sistema
- Llenguatges d’alt i baix nivell
- Interpretació i compilació de programes
- Crides a sistema i serveis de llibreries d’usuari
- Entrada/sortida i sistemes de fitxers
- Realització de pràctiques sobre Linux, en C i Python
Més informació a la guia de l'assignatura
Algorísmia i Programació II
Es comença introduint l’anàlisi dels algorismes i es presenten les eines matemàtiques per calcular-ne el seu cost. A continuació, s'utilitzen aquestes bases per estudiar i analitzar el disseny i les diferents implementacions de diversos algorismes i estructures de dades fonamentals. Alhora, s'introdueixen les eines necessàries per a poder implementar aquests algorismes en Python i/o C++ I es profunditza en l’ús de llibreries externes.
Temari
- Anàlisi d’algorismes
- Algorismes de dividir i vèncer
- Estructures de dades lineals: piles, cues i llistes
- Conjunts i diccionaris
- Cues de prioritat
- Grafs: representacions, recorreguts, camins mínims
- Realització de pràctiques amb C++ i/o Python
Més informació a la guia de l'assignatura
Teoria de la Informació
El 1948 l'enginyer i matemàtic Claude E. Shannon va publicar "A Mathematical Theory of Communication" al Bell Systems Technical Journal. En aquest treball va néixer la Teoria de la Informació, un camp completament nou, introduint els conceptes d'entropia i redundància de la informació, i els teoremes de codificació de font i codificació canal. La Teoria de la Informació proporciona un marc teòric per a la transmissió de senyals i ha estat clau en la revolució digital experimentada en les últimes dècades, ja que proporciona eines per aconseguir eficiència (compressió de dades), fiabilitat (codis de correcció i detecció d'errors ) i seguretat (criptografia) particularment adequades per al processat, emmagatzematge i transmissió de dades digitals. El curs té dos objectius principals: (1) introduir els estudiants de forma rigorosa en els punts principals de la Teoria de la Informació, incloent proves dels dos teoremes fonamentals de la compressió de dades sense errors i la codificació de la cadena sorollós; (2) presentar diverses aplicacions, incloent la compressió, codis de correcció d'errors, inferència estadística o criptografia.
Temari
- Conceptes bàsics de la Teoria de la Informació.
- Codificació de font sense errors.
- Codificació en canals sorollosos.
- Inferència estadística.
- Criptografia.
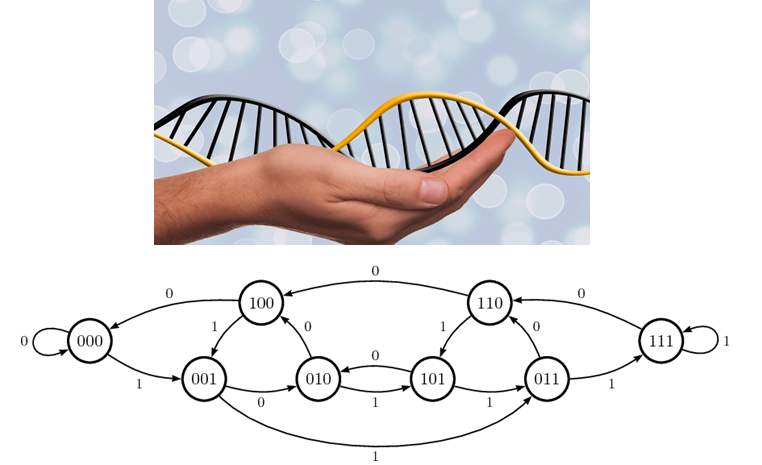
- Recuperació i verificació de dades.
Més informació a la guia de l'assignatura
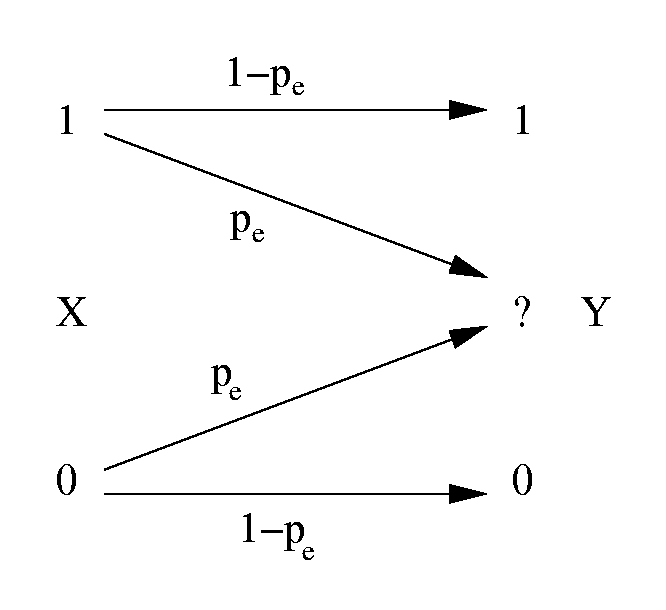
Probabilitat i Estadística II
L’assignatura completa la formació en probabilitat i estadística aprofundint en els models estadístics, en particular en els models lineals i lineals generalitzats, es tracta l’estimació Bayesiana i s’introdueixen els processos estocàstics.
Temari
- Introducció als processos estocàstics.
- Model lineal.
- Model lineal generalitzat.
- Introducció a l'Estadística Bayesiana.
Més informació a la guia de l'assignatura
Senyals i Sistemes
El conjunt de tècniques i algoritmes que permeten estudiar, detectar, transformar, processar, transmetre i classificar senyals s'anomena processat de senyal. En aquesta assignatura s'ofereix una introducció a la teoria fonamental d'aquesta disciplina. Durant el curs es caracteritzen els senyals i els sistemes en el domini del temps i en el domini de la freqüència per mitjà de la Transformada de Fourier en les seves versions analògica i discreta. El teorema de mostreig permet processar senyals analògics mitjançant tècniques discretes i així poder aplicar algoritmes computacionalment eficients. El curs introdueix el concepte de filtre i filtrat sobre senyals, especialment en el domini de la freqüència i el de correlació per determinar relacions entre senyals.
Temari
- Senyals i sistemes.
- Caracterització de senyals i seqüències, energia i potència.
- Sistemes analògics i discrets, propietats.
- Resposta impulsional i equació de convolució.
- Sistemes discrets representats per equacions en diferències.
- Convolució 2D. Resposta impulsional (sistemes FIR i IIR) i resposta freqüencial 2D
- Transformada de Fourier de senyals analògics.
- Definició i propietats.
- Resposta freqüencial.
- Exemples: Filtrat, enfinestrat, modulació.
- Mostreig.
- Teorema de mostreig.
- Fórmula d'interpolació.
- Conversió A/D, D/A.
- Mostreig 2D.
- Transformada de Fourier de senyals discrets.
- Definició i propietats.
- Transformada de Fourier 2D.
- Transformada Discreta de Fourier. DFT 1D, DFT 2D.
- Filtrat.
- Transformada z.
- Disseny de filtres. Plantilla d'especificacions. Eines de disseny.
- Filtres de fase lineal, filtres passa tot.
- Filtrat pas alt i pas baix 2D.
- Delmat i interpolació.
- Delmat i interpolació
- Canvi de la freqüència de mostreig.
Més informació a la guia de l'assignatura
Bases de Dades
L’estudiant tindrà una visió general sobre què és una base de dades, els seus objectius i principals components. Profunditzarà en els gestors basats en el model relacional de bases de dades i practicarà la creació, gestió i ús dels seus components mitjançant SQL. S’inclou una introducció al disseny de bases de dades relacionals, així com l’estudi dels diferents components d’un gestor. L’estudiant coneixerà els conceptes relacionats amb l’emmagatzematge de dades orientades a l’anàlisi.
Temari
- Concepte i models de base de dades.
- Concepte de Sistema de Gestió de Bases de Dades.
- Model relacional.
- Introducció a l’àlgebra relacional i SQL.
- Mecanismes d'accés des de llenguatges d’alt nivell.
- Introducció al disseny d’una base de dades.
- Estructures bàsiques d’emmagatzematge i accés.
- Costs dels mètodes d’accés i optimització.
- Transaccions.
- Magatzems de dades i bases de dades multidimensionals.
Més informació a la guia de l'assignatura
Algorísmia i Programació III
En aquesta assignatura s'estudien els principals esquemes algorísmics per a la resolució de problemes computacionals complexos. De forma paral·lela s'introdueixen les eines necessàries per a poder implementar aquests algorismes en un llenguatge de programació modern.
Temari
- Cerca exhaustiva
- Tractabilitat: classes de problemes P i NP
- Programació dinàmica
- Algorismes voraços
- Algorismes d'aproximació
- Metaheurístiques
- Realització de pràctiques amb C++
Més informació a la guia de l'assignatura
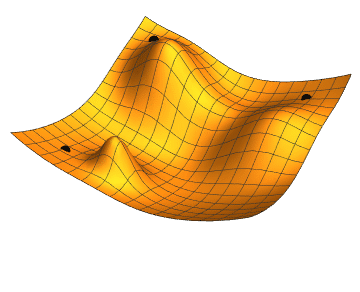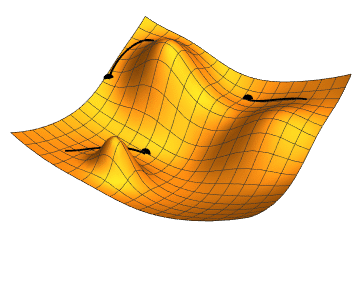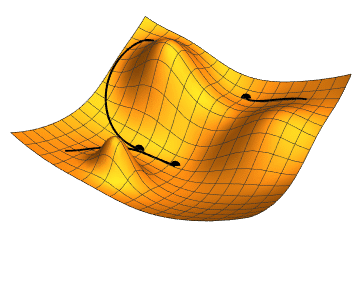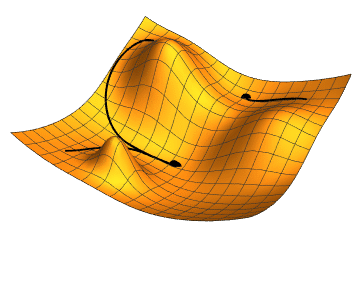
Optimització Matemàtica
En aquesta assignatura l'estudiant aprendrà a modelitzar problemes d'optimització; coneixerà les bases teòriques mínimes dels mètodes de optimització; conocerrá algun mètode d'optimització per als diferents tipus de problemes (lineals, quadràtics, enters, combinatoris); sabrà aplicar mètodes i paquets d'optimització per la solució de problemes reals; i solucionarà problemes propis de la ciència de dades (com l'entrenament de xarxes neuronals i support vector machines, clustering, etc.), un cop formulats com a problemes d'optimització.
Temari
- Optimització sense restriccions: Modelització de problemes.
- Condicions d'optimalitat.
- Convexitat.
- Direccions de descens.
- Exploracions lineals.
- El mètode del gradient o de màxim descens i variants (gradients estocàstics, etc.); velocitat de convergència del mètode del gradient.
- El mètode de Newton i variants globalment convergents (Newton modificat); velocitat de convergència del mètode de Newton.
- Mètodes quasi-Newton.
- Aplicacions: xarxes neuronals, regressió LASSO.
- Optimització amb restriccions: Modelització de problemes.
- Convexitat.
- Condicions d'optimalitat (condicions Karush-Kuhn-Tucker).
- Casos particulars: optimització lineal i optimització quadràtica.
- Mètode del símplex per optimització lineal.
- Dualitat en optimització.
- Dual de problemes lineals i quadràtics.
- Aplicacions: support vector machines.
- Optimització entera: Modelització de problemes amb variables binàries i/o enteres.
- Problemes combinatoris.
- Propietats dels problemes d'optimització entera i combinatòria.
- Mètodes de resolució: branch-and-bound i plans de tall.
- Aplicacions: clustering, k-medians.
- Programació amb restriccions.
Més informació a la guia de l'assignatura
Anàlisi de Dades
Els estudiants adquiriran un coneixement ampli de tècniques d'aprenentatge automàtic, de modelització estadística i anàlisi de dades modernes; un coneixement dels principals mètodes de visualització de dades complexes, tant tabulades com no; la capacitat d'integrar totes tècniques en aplicacions complexes, i d'usar-es fluidament en l'anàlisi de conjunts de dades grans. En particular, la capacitat de fer anàlisis, o desenvolupar aplicacions que ajudin a l'anàlisi, d'informació de xarxes socials que incloguin informació textual i hipertextual, entre d'altres.
Temari
- Exploració multivariant.
- PCA, SVD, Factor Anàlisis. Multimensional Scaling.
- Anàlisi de Correspondències Simples.
- Anàlisi de Correspondències Múltiples.
- Clustering. Profiling.
- Anàlisi discriminant amb hipòtesis probabilistes.
- Distribució normal multivariant. Distribucions muestrals.
- Linear Discriminat Analisis, Discriminació de Fisher.
- Quadratic Discriminant Analisis.
- Modelització multivariant.
- Regresió multivariant.
- Anàlisi Canònica de correlacions.
- Principal Component Regression.
- Partial Least Squares Regression
Més informació a la guia de l'assignatura
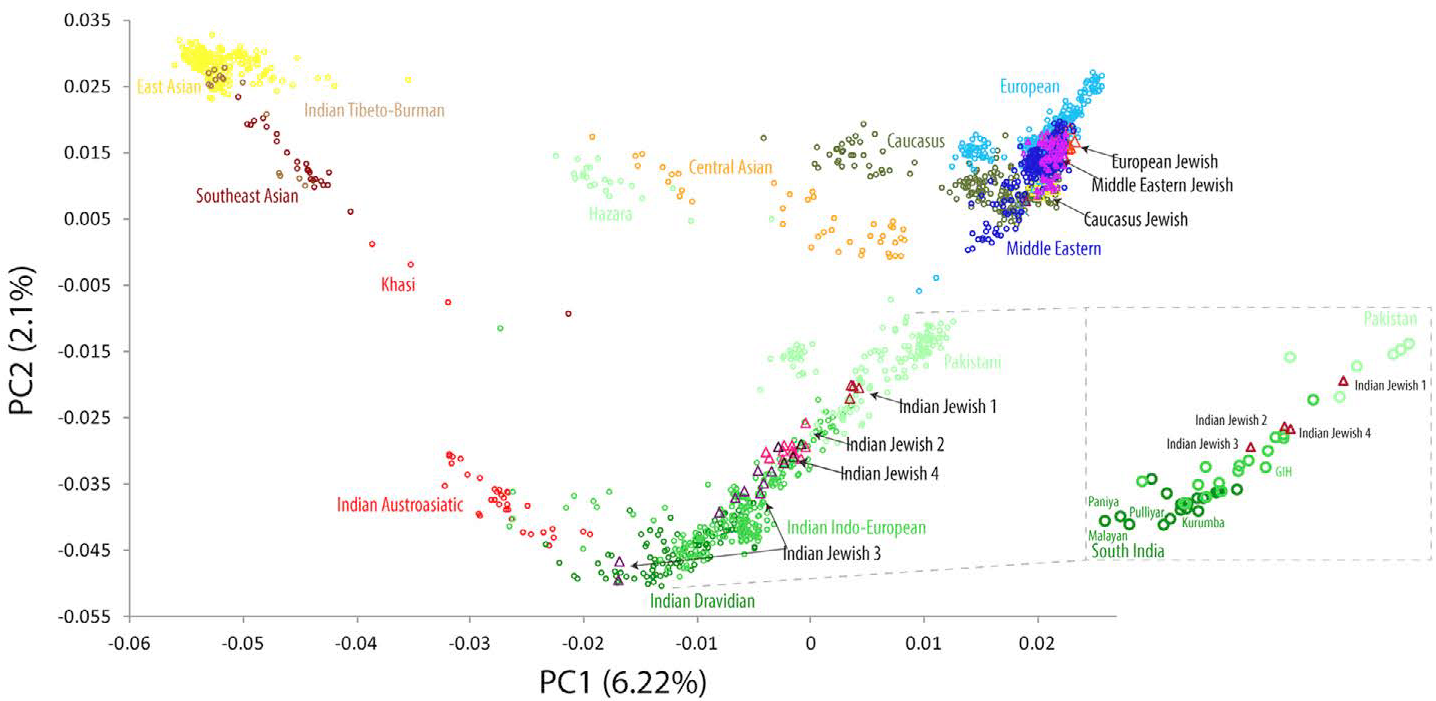
Introducció al Processat Audiovisual
Desenvolupar la intuïció del comportament dels sistemes audiovisuals i de les característiques dels senyals amb especial èmfasi en els senyals audiovisuals. Presentar els elements fonamentals del modelat estadístic de senyals. Proporcionar transformacions útils per a processar en els dominis temporals i transformats senyals discrets genèrics i audiovisuals. Desenvolupar eines de filtratge òptim per senyals audiovisuals.
Temari
- Modelatge estadístic de senyals.
- Processos estocàstics: Definició.
- Autocorrelació.
- Estacionarietat, Ergodicitat.
- Densitat espectral de potència.
- Processos discrets.
- Filtratge de processos.
- Transformacions.
- Anàlisi en freqüència.
- Transformada Cosinus Discreta (DCT).
- Transformada de Fourier Dependent del Temps. Interpretació com a banc de filtres. Efecte de la finestra. Reconstrucció. Espectrograma. Anàlisi temps-freqüència.
- Anàlisi multi-resolució.
- Wavelets.
- Anàlisi estadística.
- Periodograma. Principis d'estimació.
- Transformada de Karhunen-Loeve (KLT).
- Anàlisi en Components Principals (PCA).
- Components Independents (ICA).
- Discriminant Lineal (LDA).
- Anàlisi en freqüència.
- Filtrat òptim
- Estimació lineal quadràtica mitjana.
- Tipus de filtres: identificació de sistemes, equalització, cancel·lació, predicció i interpolació.
- Filtre de Wiener.
- Regressió lineal i mínims quadrats.
- Filtrat adaptatiu
Més informació a la guia de l'assignatura
Aprenentatge Automàtic I
L'objectiu de l'aprenentatge automàtic ("machine learning", en anglès) és el desenvolupament de teories, tècniques i algorismes que permetin a un sistema modificar el seu comportament a través de la inferència inductiva. Aquesta inferència està basada en l'observació de dades que representen informació incompleta sobre un procés o fenomen subjecte a incertesa estadística. L'aprenentatge automàtic és un punt de trobada de diferents disciplines: l'estadística multivariant, la intel·ligència artificial, l'algorísmia i l'optimització matemàtica, entre d'altres. L'assignatura es divideix en tres parts conceptuals, corresponents a tres tipus de problemes fonamentals: l'aprenentatge supervisat (regressió i classificació), no supervisat (clustering) i semi-supervisat (per reforç i transductiu). Les tècniques de modelat que s'estudien inclouen les xarxes neuronals artificials i les màquines de vectors suport. Com objectiu paral·lel està la familiarització amb l'R, un potent entorn de computació basat en programari lliure, així com aprendre a dissenyar solucions pràctiques en problemes difícils de resoldre de manera directa.
Temari
- Definició d'un sistema d'aprenentage automàtc.
- Tipus de tasques pròpies de l'aprenentatge automàtc.
- Nocions d'aprenentatge estadístic. Dimensió de Vapnik-Chervonenkis. Structural Risk Minimization
- Mètodes d'agrupament (clustering) probabilístics: k-means i E-M
- Remostreig estadístic.
- Funcions d'error.
- Selecció de variables: mètodes de filtrat multivarian.
- Mètodes lineals de regressió.
- Regularització i la seva aplicació a regresió.
- Classificadors generatius i discriminatius: classificadors Bayesians, regressió logística.
- Mètodes de conjunt (ensemble) I: bagging. Random Forest.
- Mètodes de conjunt (ensemble) II: boosting. Adaboost i variants.
- Xarxes neuronals feed-forward shallow: MLP (multilayer perceptron) d'una capa oculta i RBF (radial basis function) i els seus algoritmes d'entrenament.
- Xarxes neuronals recurrents shallow: xarxes de Hopfield i els seus algoritmes d'entrenament.
- Mètodes basats en nuclis: funcions de nucli bàsiques i Support Vector Machine.
- Introducció a l'aprenentatge per reforç (Reinforcement learning).
Més informació a la guia de l'assignatura
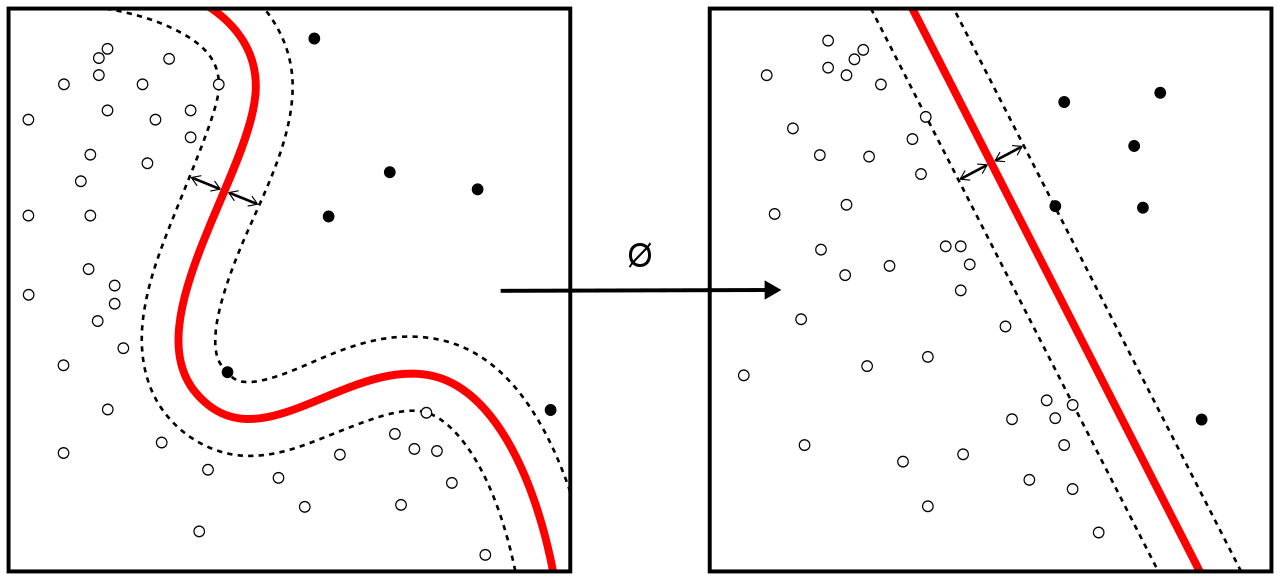
Paral·lelisme i Sistemes Distribuïts
Avui en dia l'anàlisi de dades requereix una computació a gran escala i d'alt rendiment en sistemes paral·lel i distribuïts. Aquest curs té com a objectiu proporcionar els fonaments i ús dels sistemes de computació paral·lela i distribuïda actuals. En aquest curs l'alumne comprendre el continu desenvolupament d'aquests sistemes que permeten la convergència dels algoritmes d'anàlisi avançats i les tecnologies relacionades amb els grans volums de dades per extreure coneixement de les grans quantitats de dades digitals disponibles avui en dia. Les classes es complementen amb exercicis de programació en base a problemes habituals del científic de dades i avaluar les solucions, usant sistemes paral·lels i distribuïts del Barcelona Supercomputing Center (BSC-CNS).
Temari
- Fonaments dels sistemes paral·lels i distribuïts
- Elements bàsics que conformen els sistemes paral·lels i distribuïts
- Models de programació dels sistemes paral·lels i distribuïts
- Data Science Frameworks en sistemes paral·lels i distribuïts
- Ús de sistemes paral·lels i distribuïts pels científics de dades
Més informació a la guia de l'assignatura
Visualització de la Informació
En aquest curs es presenten els elements bàsics que composen un sistema de visualització. Començant per aspectes teòrics de la percepció, passant pels tipus de problemes que es poden adreçar, i s’acaba amb el desenvolupament d’aplicacions de visualització de dades (modelat de dades, construcció de la representació i implementació de la interacció) utilitzant programari específic.
Temari
- Color i percepció.
- El procés de visualització de la informació.
- Elements bàsics d’un sistema de visualització.
- Eines pel disseny de sistemes de visualització.
- Anàlisi exploratori de dades.
- Models de dades.
- Models de visualització: Taules, gràfiques, mapes de punts, grafs....
- Dades espacials.
- Visualització de múltiples variables i dimensions.
- Manipulació de vistes. Context i enfocament.
- Reducció de la dimensionalitat.
- Treball pràctic amb D3 / Vega
Més informació a la guia de l'assignatura
Cerca i Anàlisi d’Informació
El curs presenta els conceptes i les tècniques principals per a la cerca i anàlisi d’informació en grans sistemes descentralitzats com ara la web i les xarxes socials. Partint de l“information retrieval” clàssic, s’amplien els escenaris de cerca a informació no textual i a informació enllaçada, i en què cal que el sistema faci recomanacions actives.
Temari
- Informació textual. Models de rellevància I similaritat
- Índexs i algorismes de cerca.
- Cerca a la web. Crawling
- Anàlisi basat en enllaços. Pagerank.
- Arquitectura de sistemes de cerca a la web
- Cerca d’informació no textual
- Anàlisi de xarxes socials. Mesures de centralitat. Comunitats. Tòpics. Influència.
- Classificació, agrupament i llenguatge natural, aplicacions a la cerca d’informació
- Web semàntica I “linked data”
- Sistemes de recomanació i sistemes de “query answering”
- Cerca i anàlisi distribuits
Més informació a la guia de l'assignatura
Comparteix: